Mathematics Education

What is engaged research?

Public engagement with Higher Education research (often shortened to HE-PE) is all about the different ways universities engage the wider public with their research and activities. The goal isn’t just to inform people, but to build positive, two-way relationships between universities and communities. According to the UK National Co-ordinating Centre for Public Engagement, it should involve genuine interaction and listening, with the aim of generating mutual benefit (NCCPE, 2020). Many UK academics feel a strong moral obligation to get involved in public engagement, and participation is often based on intrinsic rewards, such as wanting to share their research with broader audiences (Watermeyer, 2016), but academics also need to see how it benefits their own personal and professional development. Whilst most academic researchers agree that HE-PE should be based on a two-way relationship in practice it often follows a ‘deficit model’ approach, where academics decide what to share, when, and how, and the public is expected to just take it in (Grand et al., 2015).

School students engaging with tiling puzzles at the Open University Aperiodic Tiling exhibition

Over the last decide, universities have been encouraged to rethink how they engage with the public, to not just present research to audiences, but to work with and include publics in the creative process (Grand et al., 2015). This is where engaged research comes in, a concept coined by Open University researchers (Holliman et al., 2015). Rather than one-off events or top-down communication, it’s a more intentional and collaborative approach. Instead of academics doing the research in isolation and then sharing it afterwards, engaged research brings in community members, stakeholders, or even school students as collaborators at different stages of the research, including sometimes at the very start of the research process (Holliman et al., 2015). It’s about breaking down the barrier between expert and audience and creating a more equal, inclusive way of doing and sharing research. Researchers and the public work together to ask questions, gather data, and make sense of the results. Everyone brings different experiences and knowledge to the table and different forms of knowledge, not just academic knowledge, are treated as valuable. Engaged research is built on relationships, trust, and shared learning.

The challenge is that it is not easy to achieve engaged research. According to Holliman et al. (2017), engaged research can take more time, more effort, and is often far more labour intensive than traditional academic research. It requires planning, communication, and can require a willingness to let go of control. Barriers such as research funding, short timeframes or university policies can make it difficult to plan for engaged research. For these reasons, some researchers still prefer to continue with more established models, because they feel simpler or more familiar. This means the most common kinds of HE-PE are still one-way, ‘top-down’, events including researcher led lectures, masterclasses, and demonstrations.

Why is it important to move beyond the deficit model of HE-PE?

Whether they are aware of it or not, academic researchers in mathematics and statistics hold power over the knowledge they create through their research. For example, they not only choose what to research (though this can be constrained by research funding) but they also make decisions about how to develop this research, whether to involve non-academic stakeholders in the planning process or data collection stages (Medvecky, 2018). They also choose how the research is shared within academic and non-academic communities, including which journals to publish with, which science fairs to present at, which schools or community groups (if any) to visit etc. This means that researchers have a responsibility to consider epistemic justice,  or fairness in knowing, that is, to consider how the knowledge they create is equitably distributed and beyond that, to make sure it is created fairly.

The concept of epistemic justice was developed by British philosopher Miranda Fricker (2017) to describe the ethics of knowledge production. It describes a fairness in the way knowledge is shared, created, and valued. In simple terms, it’s about making sure everyone has a fair chance to know things, and to be recognised as someone worth listening to.

Fricker (2017) describes two main types of epistemic injustice: Testimonial injustice and Hermeneutical injustice.

Testimonial injustice happens when someone’s knowledge or experience isn’t taken seriously because of who they are, or in contrast when someone’s knowledge is overly trusted because of who they are. For example, a professor in mathematics may be considered an expert over a hobbyist mathematician, even if the topic in questions is outside of the professor’s expertise and the hobbyist has a great deal of knowledge in this area. If the hobbyist’s opinion is dismissed because they are seen as a non-expert, that’s a form of testimonial injustice.

In 2022, a retired print technician and amateur mathematician, David Smith, showed the value of non-expert knowledge by making a significant discovery in the field of aperiodic geometry through creating an aperiodic monotile: a single aperiodic tile which could tile the plane. This discovery helped solve the previously unsolved Einstein problem.

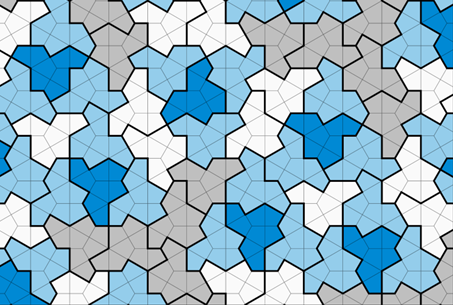
Hat tiling created by David Smith

Hermeneutical injustice is when people don’t have the tools, language, or opportunity to fully understand or express their experiences. In a mathematics and statistics research context, this might mean not being supported to ask questions, challenge assumptions, or explore new ideas. For example, when a new mathematical discovery is made, if it is shared only in academic journals, using very technical language, public audiences may not have the tools to understand or question the discovery.

When universities rely on traditional models of public engagement, groups like school students, community members, or hobbyists can be unintentionally excluded from sharing their knowledge or from being able to learn, question and critique new knowledge. Not because they don’t have anything to offer, but because they aren’t always seen as serious contributors or given the opportunity to contribute. That’s not just a missed opportunity to learn from different groups of people and to expand knowledge production and exchange, it is also a form of epistemic injustice.

Holliman (2019) suggests that engaged research can help tackle issues of epistemic injustice by opening up space for more people to be seen, and to see themselves, as knowers. It values different ways of understanding the world, not just what’s published in academic journals. And that makes research fairer, more inclusive, and often more relevant to real-life challenges.

A-level students working on mathematical research at the Open University

Further reading

Rick Holliman, Professor of engaged research, gave his inaugural lecture entitled ‘Fairness in knowing’, about engaged research and epistemic justice. You can watch and read it here: Fairness in knowing’: How should we engage with the sciences? | The Open University

References

Fricker, M. (2017). Evolving concepts of epistemic injustice. In The Routledge handbook of epistemic injustice (pp. 53-60). Routledge.

Grand, A., Davies, G., Holliman, R. and Adams, A. (2015) ‘Mapping Public Engagement with Research in a UK University’, PLoS ONE, 10(4) pp. 1–19.

Holliman, R., Adams, A., Blackman, T., Collins, T., Davies, G., Dibb, S., Grand, A., Holti, R., McKerlie, F., Mahony, N., and Wissenburg, A. eds. (2015). An Open Research University. Milton Keynes: The Open University.

Holliman, R. (2019). Fairness in knowing: How should we engage with the sciences? The Open University, Milton Keynes. Online: http://oro.open.ac.uk/60416

Medvecky, F. (2018). Fairness in knowing: Science communication and epistemic justice. Science and engineering ethics, 24(5), 1393-1408.

National Co-ordinating Centre for Public Engagement (2020) What is Public Engagement? Available at: https://www.publicengagement.ac.uk/about-engagement/what-public-engagement.

Watermeyer, R. (2016) ‘Public Intellectuals Vs. New Public Management: The Defeat of Public Engagement in Higher Education’, Studies in Higher Education, 41(12), pp. 2271–2285. Doi: 10.1080/03075079.2015.1034261.

This post is written, in both English and Welsh, by Dr Delyth Tomos, an OU Associate Lecturer who tutors on modules in mathematics and statistics, and engineering.

Delyth has recently co-led a project looking at Welsh-medium tuition in mathematics.  To learn more about the project, click here  

Ysgrifennwyd y neges hon, yn y Gymraeg ac yn Saesneg, gan Dr Delyth Tomos, Darlithydd Cyswllt gyda’r Brifysgol Agored, sy’n diwtor ar fodiwlau mewn mathemateg ac ystadegau, a pheirianneg.

Yn ddiweddar mae Delyth wedi cyd-arwain prosiect yn edrych ar addysgu mathemateg drwy gyfrwng y Gymraeg.  Er mwyn gweld mwy o wybodaeth am y prosiect, cliciwch yma.

As someone who has lived and worked in North Wales since birth, being exposed to two languages, Cymraeg/Welsh and English, is pretty much a way of life. Children are taught in both languages from an early age, and develop linguistic skills that allow them to participate fully in education, work, family and social activities in two languages, thus maximising the opportunities available to them.  Discussions in formal and informal settings are frequently conducted through both languages, switching from one to the other, and most of us do this with ease, hardly realising that what we are doing is much more complicated linguistically than we possibly realise.

Welsh landscape. Image credit David Kjaer / Nature Picture Library / Universal Images Group.

A bilingual education involves subjects being taught in both languages, and effective strategies have evolved over the decades, underpinned by a wealth of research in countries where living through the medium of more than one language is the norm (Spitzer, 2016 and Mukan et al, 2017). These strategies promote constructive learning where the use of two languages enhances a learner’s resilience and effectiveness within specific subjects as well as their language skills in general.

Learning mathematics through the medium of both Cymraeg and English encourages learners to acquire and develop flexible approaches to their studies. Understanding and learning how to solve mathematical problems requires a learner to develop a subject-specific vocabulary which needs to be incorporated within the learner’s wider language skills. In mathematics, a learner needs to be able to  describe  and interpret a problem, analyse and select relevant pieces of information from a given situation, organise the information, consider how this information may be used to address a particular problem, select and justify suitable mathematical methods, undertake various mathematical calculations and manipulations, and finally, to interpret their solutions or results in order to address the original problem.   It is clear that these strategies are complex, and it can also be seen that most of these skills are deeply embedded in language.

School sign in English and Welsh languages. Image credit David Hunter / Robert Harding World Imagery / Universal Images Group

When discussing mathematical concepts and terms in different languages, learners have opportunities to make connections with previous knowledge in both languages, and this, in turn helps them to construct their learning of mathematical ideas in both languages. Mathematical problems may be described and framed in a similar manner in two different languages, but the translation will not be exactly the same. Translation is not a matter of substituting one word from one language to an equal term in another language. Effective translation requires an equivalent adaptation of meaning in both languages in addition to syntactic flexibility and choosing suitable terms to delineate a problem in a manner that is accurate and helpful. Being creative and flexible as part of the translation process results in mathematical problems being conceptualized from two slightly different  directions, resulting in a deeper understanding of how to address problems.

Learning mathematics (and other subjects) through the medium of two languages thus provides learners with opportunities to fully engage in learning, in both their first and second language, and to engage with concepts from two slightly different directions. This in turn encourages them to become flexible, creative and resilient learners  and this naturally benefits mathematics learners.

Manteision astudio mathemateg mewn dwy iaith (Cymraeg a Saesneg)

Fel rhywun sydd wedi byw a gweithio yng Ngogledd Cymru ers ei geni, mae dod i gysylltiad â dwy iaith, Cymraeg a Saesneg, yn ffordd o fyw. Caiff plant eu haddysgu yn y ddwy iaith o oedran cynnar, a byddant un datblygu sgiliau ieithyddol sy’n caniatáu iddynt gymryd rhan lawn mewn addysg, gwaith, gweithgareddau teuluol a chymdeithasol mewn dwy iaith, gan wneud y mwyaf o’r cyfleoedd sydd ar gael iddynt.  Caiff trafodaethau mewn sefyllfaoedd ffurfiol ac anffurfiol eu cynnal yn aml drwy’r ddwy iaith, gan newid o’r naill i’r llall, ac mae’r rhan fwyaf ohonom yn gwneud hyn yn rhwydd, prin yn sylweddoli bod yr hyn yr ydym yn ei wneud yn llawer mwy cymhleth yn ieithyddol nag yr ydym o bosibl yn sylweddoli.

tirwedd Cymru. Credyd delwedd David Kjaer / Llyfrgell Lluniau Natur / Grŵp Delweddau Cyffredinol.

Mae addysg ddwyieithog yn golygu bod pynciau’n cael eu haddysgu yn y ddwy iaith, ac mae strategaethau effeithiol wedi datblygu dros y degawdau, wedi’u hategu gan gyfoeth o ymchwil mewn gwledydd lle mae byw trwy gyfrwng mwy nag un iaith yn norm. (Spitzer, 2016 A Mukan et al, 2017). Mae’r strategaethau hyn yn hybu dysgu adeiladol lle mae’r defnydd o ddwy iaith yn gwella gwydnwch ac effeithiolrwydd dysgwr o fewn pynciau penodol yn ogystal â’u sgiliau iaith.

Mae dysgu mathemateg trwy gyfrwng y Gymraeg a’r Saesneg yn annog dysgwyr i gaffael a datblygu ymagweddau hyblyg at eu hastudiaethau. Mae deall a dysgu sut i ddatrys problemau mathemategol angen i ddysgwr ddatblygu geirfa pwnc-benodol y mae angen ei hymgorffori o fewn sgiliau iaith ehangach y dysgwr. Mae angen i’r dysgwr allu disgrifio a dehongli problem, dadansoddi a dewis darnau perthnasol o wybodaeth o sefyllfa benodol, trefnu’r wybodaeth, ystyried sut y gellir defnyddio’r wybodaeth hon i fynd i’r afael â phroblem benodol, dewis a chyfiawnhau dulliau mathemategol addas, gwneud cyfrifiadau a thriniadau mathemategol amrywiol, ac yn olaf, dehongli eu hatebion neu ganlyniadau er mwyn mynd i’r afael â’r broblem wreiddiol.  Mae’n amlwg bod y strategaethau hyn yn gymhleth, a gellir gweld hefyd bod y rhan fwyaf o’r sgiliau hyn wedi’u gwreiddio’n ddwfn mewn iaith.

Arwyddion ysgol yn y Gymraeg a’r Saesneg. Credyd delwedd David Hunter / Robert Harding World Imagery / Grŵp Delweddau Cyffredinol.

Wrth drafod cysyniadau a thermau mathemategol mewn gwahanol ieithoedd, caiff dysgwyr gyfleoedd i wneud cysylltiadau â gwybodaeth flaenorol yn y ddwy iaith, ac mae hyn, yn ei dro, yn eu helpu i adeiladu eu dysgu o syniadau mathemategol yn y ddwy iaith. Gellir disgrifio problemau mathemategol a’u fframio mewn modd tebyg mewn dwy iaith wahanol, ond ni fydd y cyfieithiad yn union yr un fath. Nid yw cyfieithu yn fater o amnewid un gair o un iaith i derm cyfartal mewn iaith arall. Mae cyfieithu effeithiol yn gofyn am addasiad cyfatebol o ystyr yn y ddwy iaith yn ogystal â hyblygrwydd cystrawennol a dewis termau addas i amlinellu problem mewn modd sy’n gywir ac yn ddefnyddiol. Mae bod yn greadigol a hyblyg fel rhan o’r broses gyfieithu yn arwain at gysyniadoli problemau mathemategol o ddau gyfeiriad ychydig yn wahanol, gan arwain at ddealltwriaeth ddyfnach o sut i fynd i’r afael â phroblemau.

Mae dysgu mathemateg (a phynciau eraill) trwy gyfrwng dwy iaith felly yn rhoi cyfleoedd i ddysgwyr ymgysylltu’n llawn â dysgu, yn eu hiaith gyntaf a’u hail iaith, ac i ymgysylltu â chysyniadau o ddau gyfeiriad ychydig yn wahanol. Mae hyn yn ei dro yn eu hannog i ddod yn ddysgwyr hyblyg, creadigol a gwydn, ac mae manteision amlwg i hyn ar gyfer dysgwyr mathemateg.

References/Cyfeiriadau

Mukan, N.  et al (2017). The Development of Bilingual Education in Canada. Advanced Education, Issue 4(8) pp. 35 – 40.

Mukan, N. et al (2017). Datblygiad Addysg Ddwyieithog yng Nghanada. Addysg Uwch, Rhifyn 4(8) tt. 35 – 40.

Spitzer, M (2016). Bilingual Benefits in Education and Health. Trends in Neuroscience and Education, Volume 5, Issue 2, pp 67-76.

Spitzer, M (2016). Buddion Dwyieithog mewn Addysg ac Iechyd. Tueddiadau mewn Niwrowyddoniaeth ac Addysg, Cyfrol 5, Rhifyn 2, tt 67-76.

This post is written by Ben Leslie, winner of the Stanley Collings prize in 2024.

The Stanley Collings prize is awarded annually by the School of Mathematics and Statistics. The prize is awarded to the student who best combines innovation in devising materials suitable for learners and insightful analysis of their learning. The post is a rewritten version of his final assignment in Learning and Doing Algebra (ME322).

Congratulations Ben!

While studying the module Learning and Doing Algebra, I worked with an adult learner, who I call Ina, and who is completely blind.  Mathematics is generally taught as a visual subject so my objective was to make the tasks accessible but also to introduce concepts such as graphical illustrations that are common in the workplace.  I chose the following task from the module to introduce graphs and explain how to use them.

Task 11 What’s the story?

The following graphs provide information on two cars (car A and car B):

Comparing cars A and B

(a) Are the following statements true or false?

(i) car A is more expensive than car B.

(ii) car B is faster than car A.

(iii) car A costs less to insure than car B.

(iv) the older car costs more in road tax.

(v) the faster car costs more to insure.

(b) Write a short description for car A and car B.

(c) Use these axes to mark crosses to represent car A and car B.

Axes for comparing cars A and B

I printed Braille graphs and selected dots or distinctly shaped beads to represent the cars. I wanted Ina to develop the algebraic reasoning to understand how the distance from the origin on each axis represented the value of the axis title.

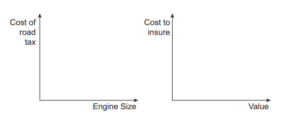
I printed a line of Braille dots for each axis and read aloud each task instruction and question. I mentioned that she need not give exact values, only its relation to the other car, for example, ‘Car A is older than B.’ She used this language when reasoning her responses to the statements. For statement (a)(i), she answered ‘False, car B is more expensive because it is younger.’ I re-phrased the question to, ‘Ignoring age, which car is more expensive?’ (I will elaborate why later, but I wanted her to practise using the y-axis.)  She finished the remaining statements without much difficulty and gave good descriptions of the cars that I recorded.

Ina’s answers

In part (c) Ina’s difficulty using the y-axis resurfaced when she tried to represent both variables on the x-axis. For example, she correctly placed car A on the x-axis for value before moving it along the same axis to identify the cost of insurance.

Using the horizontal axis for both variables

With a simple prompt she recognised and corrected it.

The last part of the question was to imagine a third car, C, describe it and add Car C to all the graphs. Ina described car C using extreme terms: “super- valuable, super old – its a vintage; very slow, massive engine, free road tax, expensive insurance”.

I influenced her choice to give car C free road tax. It would be eligible for free road tax as it was vintage, but also, it would give her a zero value to work with which I wanted to see her represent in the graph, especially because road tax was the y-axis which she found difficult. She managed this successfully.

When analysing my learner’s work, I identified three module ideas which are related to her key moments and decisions. They are relations, covariation and Invariance and change (all Open University, 2023).

Relations

I described letting my learner know that she did not have to assign values to each variable. Although there was nothing wrong with doing this, I felt it was important for her to be able to compare the cars without necessarily doing arithmetic. Inequalities can be used in algebraic expressions and being more confident with using the terminology ‘greater than’ and ‘less than’ will enable her to progress future mathematical study.  This was also an important skill to have for the true or false statements, which were expressed as inequalities.

Covariation

When my learner said car B was more expensive because it was younger.’ I re-phrased the question to, ‘Ignoring age, which car is more expensive?’ Although an onlooker may have recognised that she had given the correct answer and possibly even jumped ahead to identifying covariance, I wanted to double check that she had used the y-axis and was not just making the general assumption that new cars are more expensive than used cars. I was glad I checked, as it turned out that she had not used the y-axis. This also revealed that she had more difficulty reading the y-axis than the x-axis which is something we then worked on throughout the task.  After ensuring she was reading the graphs correctly, I revisited her first answer and explored covariance. I congratulated her for pointing out there is often a relationship between the age and value of items and explained that covariance does not imply causation. I encouraged her then, throughout the rest of the tasks, to identify if the covariations between different aspects of the cars make sense, for example, if the engine is larger,  would the max speed be expected to change? It was interesting to watch which covariances she carried through in car C. For example, she continued with age and speed varying together, but age and value varying separately as she accounted for it being vintage.

Invariance and Change

This task was set out well and allowed for my learner to not only explore different covariations, but also to change which relationships are explored. In part (c) two empty graphs were given. The change here was that the cost to insure, which was on the x-axis in the previous graph, became the y-axis in the new graph. Additionally, the value of the cars, which was previously a y-axis became an x-axis. This helped my learner ground her understanding of the y-axis as she converted the approximate distance of y-variable from the origin, into an x-variable and vice versa with the cost to insure variable.

Reflection

When choosing and preparing the tasks throughout this module, I had focused on improving my abilities to make them accessible and meaningful to my blind learner. On reflection, my preparations have improved dramatically from her first tasks, where I used random objects at hand as representations of numbers or symbols, to now where in this example I have carefully thought out how to write the task in an accessible format with clear meaning. This allowed me to follow Bruner’s modes of representation (Open University, 2023) to help use tangibility to lay the foundation for concepts which can later be simplified into Braille symbols or even calculated mentally.

I often had to apply the module concept of using variation in teaching to ensure that my learner grasped the concepts intended in the session (Open University, 2023). This would range from me needed to rephrase questions, like I did in this task, or writing new problems that would stretch my learner’s thinking. This is related to the module idea of freedom and constraint (Open University, 2023), and I would often try to introduce or remove a constraint in her tasks to  enhance the learning experience, in this task I did that more subtly by encouraging her to use free road tax for car C.

Another module concept that I focused on was conjecturing and convincing (Open University, 2023). I liked the idea of allowing my learner to create her own conjectures based on the evidence in front of her, and then by testing that, was able to convince herself she was right. I really felt this was something important I wanted my learner to experience as I didn’t want her to have my educational experience – knowing what the right answer was, without knowing  it was the right answer or  it came from.

Overall, I have been struck by how the module ideas, when combined, demonstrate a very explorative and exciting way to teach and learn algebra. Before starting the module, I was anticipating there would be one or two clear-cut, tried and tested methods of drilling algebraic concepts into student’s heads. But I have enjoyed how the learning experience has been more focused on enabling the learner to learn and discover for themselves and share that excitement with their teacher, who can also learn or observe something new in every lesson.

References

The Open University (2023) ME322: Learning and doing algebra.

Written by Lecturer in Mathematics Education, Vinay Kathotia

Here’s a mathematics puzzle: Suppose you walked up a hill at a constant speed of 3 kilometres per hour and you immediately walked down the hill taking the same route but at a constant speed of 5 kilometres per hour, then what is your average speed for the full round trip?

You can work on this using your preferred approaches, but if one asked you for your quick or intuitive answer what would it be? And how confident are you about it?

Spoiler alert! We share solutions to this puzzle below, so if you would like to work on it for yourself first, please do that before returning here.

Walking downhill. Image thanks to KimJaesub (Pixabay)

Many people when posed this puzzle propose the answer 4 kilometres per hour (kmph), though simultaneously, they are not quite sure about this answer, say compared to their answer for 3 + 5 = ? There are good reasons for their answer, and for their scepticism, and we will explore that here.

Nobel laureate Daniel Kahneman and his colleague Amos Tversky have done substantial research on human judgment and decision making. In his book, Thinking Fast and Slow, Kahneman shares some of their research and approaches. They hypothesise that our minds have two ‘systems’, System 1 produces fast, automatic/instinctive responses with seemingly little effort, whereas System 2 is slower, effortful, allocates attention and can regulate our (default) use of System 1. Moreover, System 1 exhibits ‘no sense of voluntary control’, while System 2 operations relate  to ‘agency, choice, and concentration’ (Kahneman, 2011, p.4).

We need to bear in mind that these ‘systems’ are models or metaphors, we don’t fully understand the workings of the mind, but there is substantial evidence for the patterns of thought and judgment that Kahneman outlines. What does this have to do with our puzzle? Our hypothesis is that reaching out for 4 kmph as the average of 3 kmph and 5 kmph is an instance of doing mathematics fast (System 1 thinking), whereas any unease you may have and the desire to work it out at your pace could be an expression of System 2 thinking. So how would you or did you go about solving this puzzle. Below we share two approaches, both of which align with what we would call Slow Mathematics – our preferred approach!

Make it real or realisable
Speed, the measure underlying this puzzle is a compound measure (it sets up a relationship between two more basic measures, distance and time). Research tells us that learners can find reasoning with compound measures difficult but, as mathematics is often about studying relationships between variables, working with compound measures can be critical for developing mathematical reasoning. One approach is to use numbers and units that you are comfortable using, that are realisable for you and/or make sense to you.  Notice the problem does not tell us how long (in kms say)  the trek uphill is. So could we choose a distance  that is easy to work with. It need not be realistic but something that makes the mathematics more accessible and realisable. I would suggest a 15 km trek. Why? Setting that question aside for a moment, verify that our trip uphill would take 5 hours and the faster downhill leg would take 3 hours. Notice this approach somehow does away with the ‘compoundness’, having us work with simpler numbers and units one at a time. So our total trip of 15 + 15 = 30 kms has taken 3 + 5 = 8 hours. We can now work out that the average speed is 30/8 kmph or 3.75 kmph. So not far from 4 kmph but lower than that. Is there some way we could have assessed or estimated that earlier?

Going to extremes
One approach when grappling with mathematical problems is to vary the problem, seemingly making it even more difficult, but the variation can help clarify underlying relationships. So suppose you went uphill at 3 kmph but came down at an excruciatingly slow pace (almost 0 kmph), then what would your average speed for the round trip be? Would it be close to the average of 0 and 3, say 1.5 kmph, or closer to 0 kmph, or closer to 3 kmph? Similarly, if you were to whizz down at close to the speed of light, what would your average speed be? Do explore these thought experiments and it may help you see that average speed over two equal-distance legs need not be the mean of the speeds over each leg. Which leg will you be spending more time on, which will therefore be your dominant experience – the fast or the slow one? And how will that impact the average?

Fast or slow mathematics
Traditionally, mathematics seems to reward quick answers. We assess students on timed exams, we search for and value quick algorithms. On the other hand, mathematics with understanding requires noticing what we do, using one approach and then another (… and another), using different representations and making connections. These may slow things down but may also provide a longer and more fruitful journey.

How do you think of fast or slow mathematics, or doing mathematics at all in the emerging era of generative AI? Do leave your thoughts below, and we will pick that up in a future blog. Meanwhile, take it slow!

References
Kahneman, D. (2011). Thinking, fast and slow. Farrar, Straus and Giroux.

Have you ever wondered just how long it is before a zombie shuffles into view? It might sound like something direct from a horror film, but knowing how soon you’ll need to dodge or outrun the undead could mean the difference between life, death, and – even worse – zombification!

Each year, on the first Tuesday in December, we hold our Christmas lecture for schools. This is an online event in which we invite a mathematician to talk about a current area of interest in mathematics in a fun and engaging manner to an audience of school students aged 16-18 from across the UK who are studying mathematics.

This year, we were thrilled to welcome Dr Thomas Woolley from Cardiff University, whose work in mathematical biology explores topics such as pattern formation and diffusion. In his spirited presentation on the mathematics of surviving a zombie apocalypse, Thomas expertly balances storytelling with serious mathematics, using secondary school calculus and horror-movie references to reveal what happens in the event of a zombie apocalypse.

If you’re eager to dissect the gruesome details – and pick up a few tricks for outsmarting zombies – be sure to check out the mathematics of surviving zombies with Thomas here where he explains things far better than I can!

Mathematics Enrichment

The OU Christmas lecture is an example of a mathematics enrichment event, in which our aim is to motivate students to study mathematics at university. By introducing new and exciting aspects of the subject not included in the school syllabus, we help students discover that mathematics is a dynamic and creative subject, replete with novel ideas and practical applications.

Creating an Enriching Event

One approach to planning and evaluating mathematics enrichment is to consider such events as opportunities outside the classroom to bring about “engagement” with mathematics (Santos & Barmby, 2010). In education it is common to think about “engagement” as having three aspects:

1. Behavioural Engagement

• Are learners paying attention?
• Are they actively participating?

2. Emotional Engagement

• How are learners feeling about the activity?
• Is it creating positive reactions and curiosity?

3. Cognitive Engagement

• Are learners exerting effort towards understanding the content?
• Are they understanding the advanced concepts?

Ideally, any enrichment event satisfies all three aspects.

Choosing the Right Topic

Selecting a topic that’s new and intriguing but still within reach of school-level mathematics is crucial. Too advanced or abstract, and students may feel overwhelmed or lose interest. Too simplistic, they might become bored. The ideal event blends familiar ideas (like basic calculus) with novel or popular contexts (like zombies), making it both accessible and relevant.

That’s exactly what Dr Thomas Woolley achieved:

• Thomas introduced real-world applications of mathematics to biology, such as animal patterns and swarming animals
• Thomas incorporated pop-culture references (zombies, horror-movie monsters)
• Thomas kept it interactive and playful, allowing students to contribute their own ideas about the philosophy of gothic horror

Modelling a Zombie Apocalypse

In his talk, Thomas initially took us on a quick tour of some applications of mathematics to biology, and biology to mathematics. He discussed how mathematics can be used to model swarming animals, and how it can be used to explain how stripes or spots form on some animals, showing everyone new and intriguing applications of mathematical ideas.

The inclusion of zombies wasn’t just an entertaining gimmick – there was serious maths involved. Using school-level calculus, Thomas explored diffusion processes, illustrated by simulations and videos of real experiments. The lecture provided a compelling example of how mathematical models can predict the movement of large groups, whether they’re flocks of animals or lumbering hordes of the undead.

Regarding survival tactics, Thomas demonstrated how a few strategic choices—like placing obstacles or, even better, simply running—could mean the difference between escape and joining the ranks of the zombies. Who knew calculus could save your brains?

Zombies might be fictional, but the underlying mathematics is very real—so keep your wits (and your brain) about you, and who knows what you’ll discover about the living world and beyond!

We hope this lecture inspired you to explore the applications of maths to real and fictitious scenarios. Have questions, comments or ideas? Share them below or connect with us on X and BlueSky @OUMathsStats.

Eager to get your school involved? Don’t hesitate to reach out to us at STEM-MS-Outreach@open.ac.uk. We’d love to hear from you!

Dr Andrew Neate, External Engagement Co-Lead, School of Mathematics and Statistics

Key Takeaways

• The OU Christmas Lecture 2024 featured Dr Thomas Woolley, who explored the mathematics of a zombie apocalypse using calculus and mathematical modelling.
• This event exemplified a successful mathematics enrichment activity, achieving behavioural, emotional, and cognitive engagement among students.
• Through the creative use of a pop-culture topic (zombies), familiar mathematical concepts (calculus) and engaging storytelling, Thomas delivered an inspiring and effective learning experience.

Santos, S. & Barmby, P., 2010, Enrichment and engagement in mathematics. In Proceedings of the British Congress for Mathematics Education April 2010. (https://bsrlm.org.uk/wp-content/uploads/2016/02/BSRLM-IP-30-1-26.pdf )

Everyone loves a puzzle, don’t they?!

One of the pulls that drew me to maths is the satisfaction that comes from solving problems, that, and the fact it is fun!

In the May 2024 edition of the maths and stats (M&S) student newsletter, OpenInterval, there were two puzzles posed, sent in by one of our M&S associate lecturers, Bob Vertes:

Here’s my approach to Puzzle 1.

The use of different letters for the digits means 4 different digits, moreover single digits. This narrowed down my possibilities to the ten digits, 0 to 9.  Reflecting now, there are still a large number of options – over 5000 ways (permutations) of selecting 4 different digits from 10:

More information definitely required to reduce the possibilities!

I figured I would just start simple and try some values to see what happened.

Notice my use of the word ‘figured’. Figuring in this sense means to think or consider but can also mean to calculate; perhaps my choice of language is influenced by the fact I am solving a maths problem.  I also use the word ‘see’ – I am looking at the problem and noticing what happens when I try something; it is important to pay attention to what is happening to make some sort of structured progress, rather than just haphazardly working through a myriad combination of digits. This can be seen as an example of “Noticing Structure”, a module idea developed in our ‘Learning and Doing Algebra’ (ME322) module.

I began by summing the units column, just as taught when learning column addition.  This led me to think about extra digits to consider, those that get ‘carried over’. For the thousands digit in the answer to be a 2, I would need a 1 carried over to combine with my existing 1.  Alternatively, ‘A’ would need to be 2 and nothing carried over from the hundreds.  ‘A’ could not be larger than 2, possibilities reduced by 80% in one move!

Note: automatic assumption I seem to have made without realising, ‘A’ cannot be 0.

I moved my attention to the units column; what would happen if ‘A’ was 2?

Look at the hundreds column. If ‘A’ is 2 then A + B + ‘anything carried’ would need to end in a zero but this would force a carry over into the thousands which is not wanted.

‘A’ cannot be 2.

Confirmation, ‘A’ should be 1.

Possibilities halved.

For the thousands digit in the answer to be 2, another 1 carried from the hundreds column is therefore needed. At this point I merrily proceeded to find that ‘B’ is 9, only for my confidence to be shaken at a later stage.

With my certainty shaken, I continue carefully.

If I can fix ‘B’, my remaining possibilities will be reduced significantly.

A final box confirms I am certain with my solution but spot the little doubt that has crept in with my question.

Mathematics is about confidence, but it is also about questioning and analysing and unpicking; all mathematical thinking.

As a maths teacher for many years, I am only too aware of and, always intrigued with, the many different methods pupils use to approach and solve problems.  Whilst we can demonstrate particular ways to solve a problem, there is usually no single correct way.  By looking at the approaches of others, we develop our own understanding of maths and its interconnectedness making links between our existing knowledge and knowledge, methods and ideas that may be new to us.

The next time you see a puzzle that needs solving, rather than rushing to get to the answer, take time to notice the steps you take along the way.

Now for Puzzle 2…

Written By Dan Rust, Student Research Bursaries and EPSRC Internship Coordinator, and Ethan Shallcross, OU Research Bursary student.

A version of this article will also be available in the OU Open Interval newsletter.

Every summer,  the Open University (OU) school of Mathematics and Statistics hosts research placements for undergraduate students from across the world, giving them the opportunity to contribute to contemporary mathematics research. Projects are supervised by one or more experienced researchers in our school, covering topics in pure and applied mathematics, statistics and the history of mathematics. These include our own research bursary scheme and EPSRC DTP Vacation Internships.

This year, we had more students than we’ve ever had before, with a total of 10 undergraduates conducting research in a range of areas including: translating ancient Arabic mathematical texts; understanding the combinatorics of swarms of robots on a network; developing games that teach environmental dynamics; enumerating algebraic objects called ‘friezes’; identifying election fraud in the 2024 Venezuelan presidential election; and statistically analysing air quality data.

While most students met with their supervisors online, having weekly video chats and exchanging regular emails, some were able to visit the OU Milton Keynes campus at Walton Hall to work with their supervisors in person.

At the end of August, we celebrated a successful summer of research by hosting a hybrid event where many of the student researchers gave short presentations about their projects. It really was a joy to see the huge variety of activity that had taken part over just a short couple of months and the school couldn’t be prouder of each of the students that took part.

A great deal of work went into these placements. The students themselves showed incredible resilience in working on challenging problems, most of whom had no previous experience of research, and our school supervisors worked extremely hard to introduce their student researchers to the world of academic research in mathematics, statistics and history, helping them to achieve feats that include a variety of academic papers, talks and posters at international conferences, the awarding of external grants, blog posts for scholarly societies and more.

Below is an account from one of our 2024 students:

Ethan Shallcross 

Last December, I gratefully received one of the OU’s student research bursaries to work on a project which can be summarised as follows. Imagine stationing robots on a subset of the nodes in a network, which are permitted to move to adjacent nodes over a sequence of timesteps. You could think of the robots as delivery robots (like those found in Milton Keynes for delivering food) and the nodes as delivery locations. We were investigating the maximum number of robots able to visit all the nodes, whilst requiring that they can always communicate freely. We considered different variants of this problem such as requiring each node to be visited by each robot, allowing all the robots to move at each timestep, and altering the conditions needed for free communication.

Robots exploring a network when using one possible definition of ‘free communication’ 

As you might expect, I explored lots of fascinating new mathematical ideas. But I also improved my ability to communicate effectively. My supervisor provided helpful advice about writing proofs formally, clearly, and concisely. I enjoyed discussing my work with others during online video calls as well as through emails and texts. Whilst attending meetings with the combinatorics research group, I learned about other people’s work and had the chance to present my findings. I had the pleasure of working with mathematicians from both within the OU and other universities in Indonesia and Slovenia. I am thankful to have had the opportunity to meet and collaborate with so many people.

Over the course of the 8 weeks, I really got a feel for what doing research is like. This even included assisting with peer-reviewing a paper before its publication – an unexpected but very insightful opportunity. I liked learning about the new results and thinking critically about the proofs to provide feedback for the authors.

I experienced the lows of finding an issue with a construction at the final check, but also the highs of solving an open problem from the literature and proving new results. I gave a talk about these results at The International Conference on Graph Theory and Information Security VI – a great experience. The work will hopefully form part of a paper to be published, which I think is very exciting! But the hours spent toiling with different problems were interesting and fulfilling, regardless of the outcome.

A screenshot from a computer program that I wrote during the project.

I thoroughly enjoyed my research bursary experience and have learned a lot. It has confirmed to me that I would like to pursue a PhD after I finish my MSc next year. I would urge any student at the OU thinking of a career in mathematical research to apply for the next round. Finally, I would like to thank James Tuite for his advice and support, all the researchers and students that I have worked with, as well as the School of Mathematics and Statistics for the opportunity.

If you are an undergraduate student and are interested in taking part in a summer research project in 2025, keep an eye out for announcements and updates on the following pages:

Mathematics & Statistics Summer Research Bursaries – https://www5.open.ac.uk/stem/mathematics-and-statistics/research/student-research-bursaries (application deadline approx. December 2024 – OU students only)

EPSRC DTP Vacation Internships – https://stem.open.ac.uk/research/research-degrees/epsrc-dtp-doctoral-training-partnership/epsrc-dtp-vacation-internships (application deadline approx. March 2025 – open to external students)

The “Learning from Improvers” project was an in-depth study of 12 Open University undergraduate students who were identified as ‘improvers’ on mathematics education modules. These students were interviewed about the difficulties they experienced and supportive strategies they used while learning to write reflectively about mathematical activity as part of their module assessments. The findings from the project have already been incorporated into the production for two new modules, resulting in a new integrated approach to assessment, including new assessment designs, additional teaching about writing, and modelling ways of analytical thinking.

You can read the full report of this project on the eSTEeM website here.

*Note: the names in this blog (and full report) are pseudonyms and not the real names of the student participants.

Why did we carry out this study?

Mathematics Education (ME) modules involve reflective writing, a type of writing which applies academic analysis to personal practice. Writing for ME modules therefore requires a different approach to writing for either straight mathematics or humanities and arts subjects, as it involves combining specific inter-disciplinary elements. Students entering our level 3 modules, many with mathematical rather than education backgrounds, need to develop these ways of thinking and writing to succeed in their assignments. We know from speaking to students and tutors on our modules that students find reflective writing particularly challenging and we have long been interested in learning how to help them to develop and improve this skill.

We reasoned that our support for students in this new approach to writing needed to be strengthened and felt that the most relevant experiences to understand were not necessarily those of the most successful ME students, but those who had improved their marks during a ME module. So we set out to investigate what it was that helped those students to improve.

What did we find out?

Through interviewing our student improvers, we gained some insight into what it is like to be a student on our ME modules. Thematic analysis of the interview transcripts revealed some of the key difficulties faced by these students whilst working through ME modules, and the approaches they found most beneficial in their improvement in written assignments.

Difficulties

Through our analysis we identified three key themes in the difficulties reported by students in our sample:

• difficulty with mathematics
• difficulty with writing
• difficulty with the unfamiliarity of the module and assignments

Support 

Four key themes were identified as being supportive to student improvers:

• personalised support
• alternative explanations
• supportive ways of working
• support from module resources.

What does this mean for our students?

We have used the insights gained from interviewing the student improvers to help make changes to our new ME modules to support all students in improving their reflective writing. This has included:

• developing an integrated approach to assignments,
• narrowing the focus of early assignments,
• explicitly teaching about writing,
• modelling reflective ways of thinking.

The major change to module content was integrating assessment activities as part of study. Our two new ME modules (ME321 and ME322) each have a detailed activity planner and time for preparing assignments is built into this. Drawing on the improvers’ emphasis on ‘having two goes’ at assignments, preparation activities for each assignment start 4-6 weeks before deadlines and each question has scheduled time for starting and separate time for finalising. Reading feedback from assignments is also a scheduled activity before each new assignment, again considering the improvers view that reading and re-reading personalised feedback was a supportive way of working.

Improvers had expressed the value of having a summary of module ideas to refer to when planning and writing. The new modules therefore include an interactive ‘Module ideas map’ which allows students to find a short definition of each idea and where it is first mentioned.

Some changes have been made to module assignments to narrow the focus. For example: for the first assignment in ME322 students only write about their own mathematical work, and do not analyse learners’ work until the second assignment. The idea is to build up the level of challenge along the module, allowing time for development of understanding of module ideas and of a reflective voice.

In response to students reported unfamiliarity with writing analytically and reflectively about mathematics, new content has been written for each module, giving explicit advice about writing, including reading about the difference between writing types and structuring paragraphs.

The last findings that directly informed module design were the universal request for sample assignments, the critique of existing videos, and the improvement associated with seeing the value of the process. In addition to written resources about writing reflectively and analytically, other resources have been developed to support students’ writing through modelling ways of thinking. These include videos of school-aged children working on mathematics ‘live’ and interactive forum activities. These allow students to develop their analytic approach by providing examples close to their own experience of working with learners, but with the added value that these experiences can be shared with other students and discussed openly on the forum. These forum activities also allow for students to give peer feedback and to learn from other perspectives than their own, or their tutors. In Learning and Doing Geometry, students are asked to take part in such forum activity as part of their first assignment, increasing the participation in the overall cohort.

For us, the value of the Learning from Improvers project has been in using students’ knowledge to inform and improve future teaching.

We are lucky to be able to introduce two new tutors joining our Mathematics Education team as tutors this academic year, and this feels like a good opportunity to reintroduce you to the other tutors who are currently working on ME620, ME321 and ME322. No doubt you will get to know them yourself through tutorials and forum discussions.

Luke Bacon 

I’ve been teaching with the OU for just over two years on other Maths modules, and am really pleased to be joining the team on ME322 this year.

I studied Pure Maths and then completed my PGCE with the OU, before working in and around schools across London and managing a series of university outreach programmes for students from disadvantaged backgrounds. I spent some time at DfE working on Higher Education policy (ask me about the student finance system!) and have worked with lots of teachers on maths-specific CPD projects, as well as teaching on a specialist STEM PGCE course.

I also work in consulting, helping to make public services (education, healthcare, and others) a little bit better for everyone, and in my ‘spare’ time I write and examine A-level Maths and Further Maths.

Kellee Patterson

I am lucky enough to have had the privilege to teach mathematics to 11-18 year olds for a quarter of a century leaving the secondary classroom in 2022.   Teaching mathematics is both fascinating and frustrating but, most of all, fun.  Fun and enjoyment was the reason I became a maths teacher with my main goal being to make maths accessible to students by helping them see the beauty and relevance of mathematics.   

In addition to maths leadership in my teaching career, I worked with trainee and new teachers as the whole school lead for Initial Teacher Training (ITT) and Early Career Teachers (ECT) (was Newly Qualified Teachers (NQT)).  Working with those at the beginning of their career is a joy and it is a real pleasure to see so many enthusiastic and determined people achieve success as they start out in teaching. 

My undergraduate maths degree and PGCE are from the University of Exeter and then, whilst teaching, I gained a masters in education from the University of Winchester.  Working full-time whilst also studying is quite the juggling act particularly given the term time working intensity as a teacher.  I take my hat off to those of you studying whilst working. 

I now teach as an Associate Lecturer (AL) for the OU on MU123 Discovering mathematics, M140 Introducing statistics, M248 Analysing data and recently ME321 Learning and doing geometry.  I came to the OU through studying and started taking modules in 2018 before becoming an AL in 2020.  My original goal of making maths accessible to all has not changed and I hope, through my work with the OU, I can continue to encourage others to enjoy mathematics and statistics. 

When I am not doing maths, I enjoy travelling, cooking and walking (I am a Duke of Edinburgh Leader and still help with expeditions at my previous school).  I enjoy learning languages and am currently trying to teach myself Spanish.  Recently, I bought myself a keyboard in a bid to try and rekindle my piano playing skills from when I was a child – this one is definitely a work in progress that requires much more practice!  

Barbara Allen

My school teaching career was in middle schools in Worcestershire where I specialised in mathematics. I developed an interest in girls’ attitudes to mathematics and that became the focus of the dissertation for my MEd. My PhD focuses on Pupils’ Perceptions of Mathematics Classrooms and found the ways that pupils think they learn most effectively.

In 1994, I moved to the Open University as a Research Fellow and in 2000 I became the Director of the Centre for Mathematics Education. I continued as the Lead Academic for Mathematics Education until my retirement in May 2017.

I have written on a large number of OU modules from Access to Masters Level. For some reason, I always ended up writing the sections on fractions!

I am the co-author of the children’s book series The Spark Files and the writer of the children’s radio series The Mudds starring Bernard Cribbins and Mark Benton. Now available on iTunes!!

My main hobby has always been playing the clarinet. I play in Bewdley Concert Band and also play alto saxophone in the Wyre Forest Big Band. Now that I am retired, I am learning to play the xylophone and threatening to learn the drums. I also volunteer at Bewdley Museum and work with school groups that are learning about WWII.

Thabit Al-Murani

Hello, I am Thabit and I am an associate lecturer teaching on the ME322 course.

I have been involved in maths education for 25 years. Over this time, I have been a teacher, head of department, researcher, and more recently I started my own freelance business offering maths education consulting and specialised tutoring. My work has offered me the opportunity to live and work in several countries including the US, Sweden, Australia, Malaysia, and the UK.

I have a DPhil in Mathematics Education and my research interests are variation theory, the teaching and learning of algebra, and SEN mathematics education.

Ian Andrews

Hello, I’m Ian and I joined the OU as an Associate Lecturer in 2022.

I studied Maths and Statistics at university and once completed, I worked in data analysis in London for several years. Wanting a change of career, I started a PGCE in 2007 and have been a maths teacher ever since!

In 2015 I joined an 11-18 comprehensive secondary school in West Sussex as Head of Maths and member of the senior leadership team. I have also worked with the Sussex mathshub and lots of locality schools to improve maths in Sussex.

In 2019 I joined AQA (alongside my full time head of maths role) as Chair of Examiners for GCSE maths, GCSE statistics and L2 Further maths. This work involves running training and events for AQA and helping set grade boundaries for their exams.

I really enjoyed learning again when I took my PGCE and in 2013 I completed an MA in Education studies. Engaging with academic research whilst being a teacher has been hugely beneficial to my practice and my department.

When not teaching I enjoy music, playing football, running and acting as a taxi service for my 2 children.

Nick Constantine

Hello everyone, I am Nick Constantine associate lecturer for the Open University, I tutor on ME620, ME321 and ME322.  I also tutor on MU123 and MST124. I have been working with the OU for 9 years but I also used to tutor on the PGCE course from 2000-2002. I have had a very mixed career. My first degree was Astronomy and Astrophysics at Newcastle University, I then joined the Royal Navy as aircrew for a little while. I left way back in 1989 and did several ‘gap’ jobs before retraining as a Mathematics teacher and PE teacher.

My teaching career followed the standard path up to Deputy Head/acting Head but I always attended many mathematics training weekends with the ATM.  I also used to attend the MEI further mathematics conference in Nottingham for a few years. I was a Head of Mathematics in a 13-19 high school in Northumberland from 1998-2004 and enjoyed the process of organising and planning activities that reflected the fundamental philosophy of the OU ME(x) modules.

I also studied for a Master’s in Education from 2000-2002, one of my dissertations was ‘conjecture and proof in the most able’ (ME822), I really enjoyed designing my own research project and had a wonderful class to try some tasks with.  For me, if you can change the language of the mathematics in the classroom from a didactic controlling language to an atmosphere of questioning, conjecturing with learners and investigating relationships then you are really at the top of your game!

I now work part time as a teacher and OU lecturer.  I also work as a running and yoga coach and operate a small business where I organise retreats and workshops for private groups in Europe and in Scotland. Other hobbies are reading, radio 6 music, cooking and doing Maths problems!

Tom Cowan

I have been an Associate Lecturer with the OU since 2008 when I worked on the MEXR624 summer school each year in Bath.  When that ended I was lucky enough to be offered a chance to work on an earlier maths education module. I currently tutor on all the modules which we offer in the Mathematics Education suite of modules at Level 3 (ME620, ME321 and ME322) and also E209 – Developing subject knowledge for the primary years.

I completed my Master’s Degree with the OU in 2010 so remember what it was like to study at a distance and cramming in study whilst juggling other things in life.

My full-time role is as the Programme Lead of an initial teacher education programme at the University of Plymouth. I support the education and development of new Primary teachers on the BEd and PGCE – looking after those students with a specialism in mathematics.  Prior to this I was primarily involved with working with Secondary and Primary schools to support them with mathematics in challenging inner-city schools around Manchester and Salford.

I’ve never really left education and have found my next challenge in aiming to complete my Doctorate in Education in 2026! Hopefully I’m well on my way to becoming Dr. Cowan!

When I have some spare time, I enjoy going to the theatre, supporting Liverpool FC and Widnes RLFC and work as an officer with the Boy’s Brigade which keeps me in touch with further voluntary work (I did say spare time right?)

Jeffrey Goodwin

As well as being an Associate Lecturer for ME321, I also tutor on ME620. I first worked as a tutor for the OU in the 1980s on EM235 Developing Mathematical Thinking and returned to my current role of Association Lecturer in September 2014.

I was a classroom teacher for 10 years, working in Secondary and Middle schools. I moved into the advisory service in 1980 as Head of the Hertfordshire Mathematics Centre. I worked in Initial Teacher Training and running CPD courses for teachers; being head of mathematics education at Anglia Polytechnic University. For four years from 1986, I worked for the National Curriculum Council on a curriculum development project: Primary Initiatives in Mathematics Education (PrIME). I have always had an interest in assessment and testing and in 1998 was appointed to establish and lead the Mathematics Test Development Team at the QCA. We developed the end of key stage tests and other optional tests for all three key stages. I was in this role for eight years and then moved to become Head of Research at Edexcel and then Pearson Research and Assessment. In 2010, I became an independent consultant and worked with schools on making changes, particularly engaging with Japanese Lesson Study. For four years I was the Programme Director for the King’s College London MaST course.

I have seen it as important to make a professional contribution to education. This has involved being Secretary of the Mathematical Association, a member of the Royal Society Mathematics Education Committee and Chair of the coordinating committee for Primary Mathematics Year 1988. I have also been chair of governors of a primary school.

I have two main research interests: the role that Lesson Study plays in the profession development of teachers; and, a member of the research team at the UCL Institute of Education looking at The Nature, Prevalence and Effectiveness of Strategies used to Prepare Pupils for Key Stage 2 Mathematics Tests, a project funded by the Nuffield Foundation.

Rebecca Rosenberg

Hello. I have been working at the Open University since 2019, mainly on the development of the new Maths Education modules. 2022 is the first year I will be tutoring on one of these modules, and I’m really looking forward to putting all that hard work into practice!

Before joining the Open University, I worked as a maths education publisher, and before that I worked as a secondary maths teacher in Suffolk. I’m particularly interested in the way people talk about maths – both inside and outside the classroom; how do we form questions in maths lessons? How is maths discussed in popular culture and media?

In my spare time I knit, sew, cook, garden and binge-watch American high-school tv shows.

Jim Thorpe

I became a mathematics teacher through the accident of joining Bill Brookes’ PGCE course: suddenly I realised that much mathematical thinking could emerge from humble beginnings, numerical or geometrical, and realised that mathematics could make a major contribution to the intellectual and social development of adolescents if they were encouraged to function as young mathematicians within what John Mason calls a ‘conjecturing atmosphere.’

I have been committed to mathematics education for a long time, in the secondary classroom and then in a variety of ways supporting the work of mathematics teachers. My current occupation is mainly tutoring in mathematics and education, mathematics, and engineering for the Open University.

I am alarmed by much of what I see under the heading of teaching mathematics but remain unrepentant in proposing something richer than the all-too-frequent ‘training’ metaphor of communicating mathematics.